The Lorentz attractor is generated by a set of differential equations which model a simple system of convective flow.  In a paper published in 1963, Edward Lorentz demonstrated that this system exhibits chaotic behavior when the physical parameters are appropriately chosen.

The Lorenz system is deterministic, which means that if we know the exact starting values of  variables then in theory we can determine their future values as they change with time. Lorenz demonstrated that if we begin this model by choosing some values for x, y, and z, and then do it again with just slightly different values, then you will quickly arrive at fundamentally different results. In real life we can never know the exact value of any physical measurement, With these results, Lorenz shocked the mathematical and scientific community by showing that a seemingly nice system of equations could defy conventional methods of prediction. This is called chaos, and its implications are far-reaching, especially in the field of weather prediction.

The Lorenz attractor is an example of a strange attractor.  Strange attractors are unique from other phase-space attractors in that one does not know exactly where on the attractor the system will be.  Two points on the attractor that are near each other at one time will be arbitrarily far apart at later times.  The only restriction is that the state of system remain on the attractor.  Strange attractors are also unique in that they never close on themselves — the motion of the system never repeats (non-periodic).  The motion we are describing on these strange attractors is what we mean by chaotic behavior.

The set of equations describing this behavior are:

x’ = σ(y – x)
y’ = x(r – z) – y
z’ = xy – bz

where the three parameter  σ , r, b are positive and are called the Prandtl number, the Rayleigh number, and a physical proportion, respectively. It is important to note that the x , y , z are not spacial coordinate. The ”x is proportional to the intensity of the convective motion, while y is proportional to the temperature difference between the ascending and descending currents, similar signs of x and y denoting that warm fluid is rising and cold fluid is descending. The variable z is proportional to the distortion of vertical temperature profile from linearity, a positive value indicating that the strongest gradients occur near the boundaries.

when σ=10, r<1, and b= 8/3 is chosen the plot look like this

when σ=10, r=1, and b= 8/3 is chosen the plot look like this

when σ=10, r>1, and b= 8/3 is chosen the plot look like this

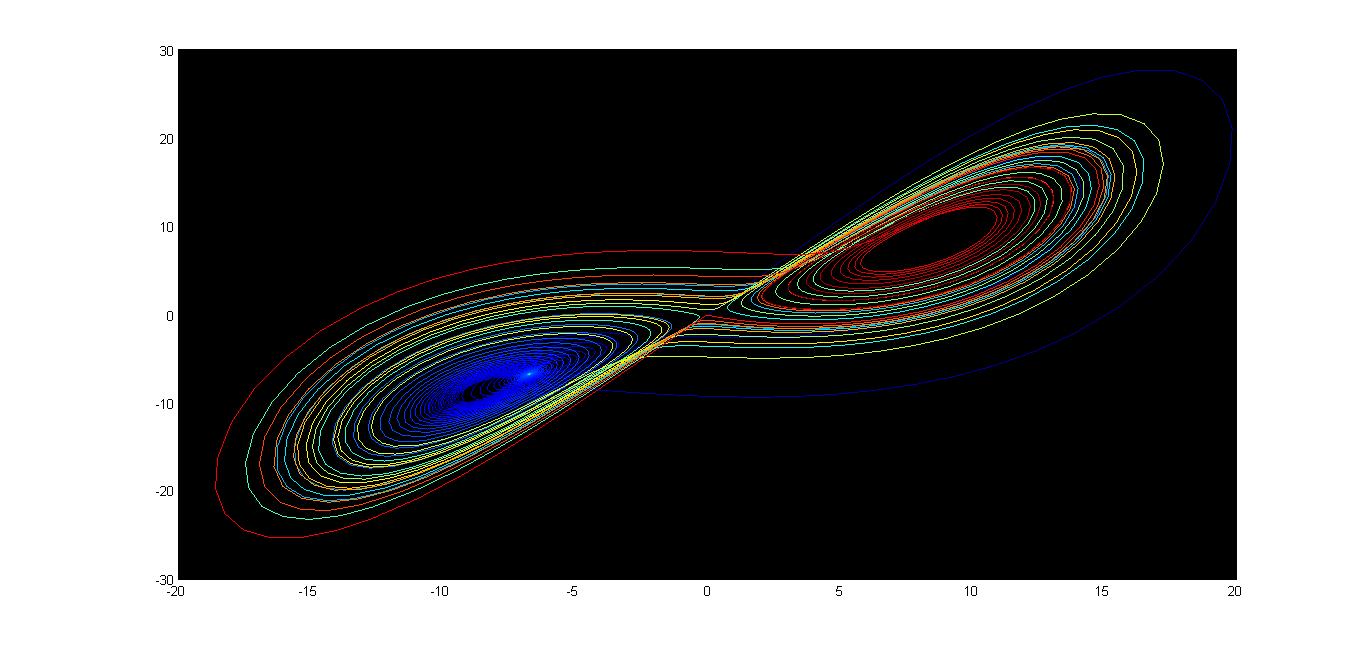
when σ=10, r=28, and b= 8/3, the Lorenz system has chaotic solutions (but not all solutions are chaotic). The set of chaotic solutions make up the Lorenz attractor, a strange attractor

The Lorenz attractor is difficult to analyze, but the action of the differential equation on the attractor is described by a fairly simple geometric model.